Nem, nem a Túró Rudika húzta keresztbe a diákokat az érettségin – hanem a térgeometria. Pedig ez lehetett volna az egyik legbiztosabb pontja azoknak, akik munka és család mellett érettségiztek. Megmutatom, hogy miért.
A 2025-ös matekérettségi után ellepték a netet a kétségbeesett kommentek:
„Szerintem a Pöttyös perelje be a feladatgyártókat, mert ezek után sokan megutálják a rudijukat.”
„Mennyi a csokibevonó? Ez most komoly?”
A diákok a 16–18. feladatok környékén rendre megijednek, mert „ott jön a neheze”.
És valóban: a térgeometria ezek egyikében mindig ott van.
„Na, azt biztosan kihagyom.”
De ha te már dolgozol, háztartást vezetsz, és felnőttként tanulsz –
akkor számodra ez luxus lenne.
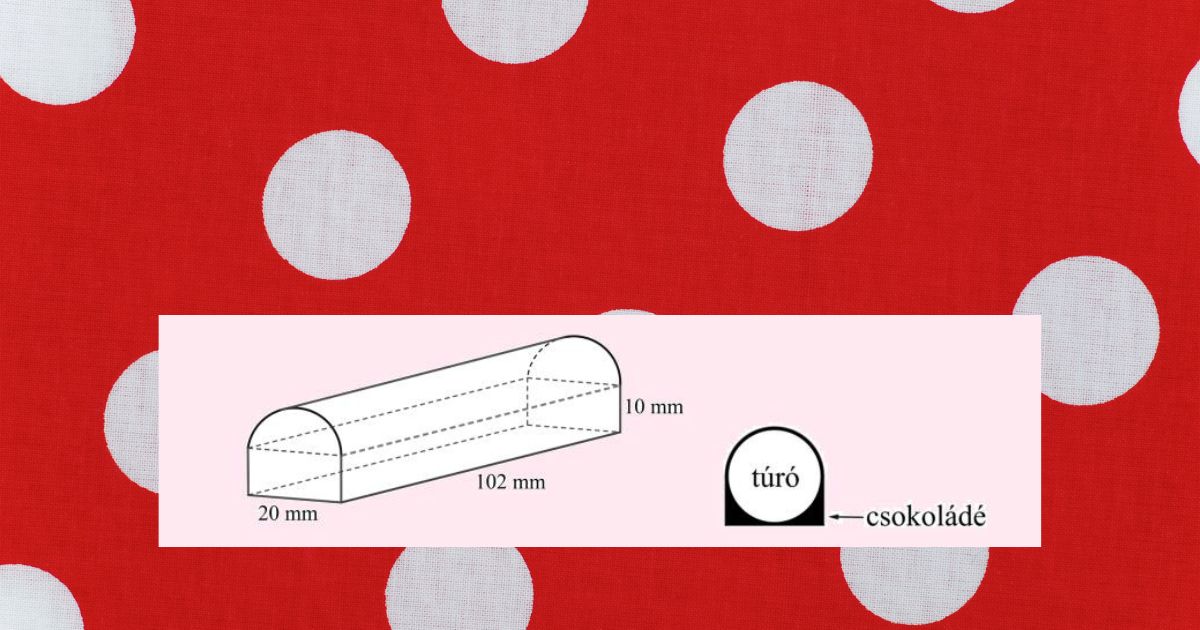
„A desszert készítésekor egy 18 mm átmérőjű, 100 mm hosszúságú lehűtött túróhenger köré csokoládébevonatot dermesztenek.
A kész desszert alakja egy 20 × 10 × 102 mm-es téglatest és egy 20 mm átmérőjű, 102 mm hosszú félhenger egyesítésének tekinthető.
Mekkora a csokoládébevonat térfogata?”
Ez a példa első ránézésre valóban „félelmetes” lehetett – de csak annak, aki nem érti, mi az, hogy térfogat.
Sőt: sokaknál már az „átmérő” szó is elbizonytalanította a megoldást.
És ha ehhez még mértékegység-átváltás is társul, máris teljes a káosz – és itt kellett is a válaszhoz.
Pedig ez a példa pont az a típus, amit nem lenne szabad kihagyni.
Miért?
Ez a térgeometriás példa például 7 pontot ért.
Simán lehet, hogy az első feladatrész gyerekjáték lett volna – de ha kihagyod az egészet a térgeometria miatt, akkor bukod a könnyűt is, ami esetleg ott lett volna mellette.
Ezért kérlek, engedd el egy pillanatra ezt a közhiedelmet, hogy a térgeometria túl nehéz.
Tér–fogat. Ami befogja a teret.
Ha főzöl – leves, pörkölt, befőtt – biztos kerültél már olyan helyzetbe, amikor át kellett önteni valamit egy másik fazékba.
Aztán mondjuk nem fért.
Egy tanítványom mesélte:
átöntötte a levest egy magasabb, keskenyebb fazékba – és nem fért bele.
És akkor esett le neki először:
A fazékba beleférő leves mennyisége = térfogat.
És ugyanez történt a Túró Rudis példában is.
levonod a túrós rész térfogatát (ami egy henger volt) – megkapod a csokibevonat térfogatát.
Logikus nem? Nézd meg a képet, hogy jön ki a csokirész!
De hogy meg is oldd a példát, értened kell a szavakat.
De ha átmérőt adnak meg – neked ki kell számolnod a sugarat, mert annak a jele a képletben az r. Az átmérő jele a d.
Mi vaaan?
És ez az a pont, ahol a legtöbb felnőttnek már korábban is elakadásai voltak. A kezdetnél.
És akkor még ott a mértékegység is.
Milliméter, centiméter, liter, köbcenti –
elég, ha nem tudod, hogy 1 liter = 1 dm³ –
sokszor már ugrik is az egész feladat.
Ezért mondom:
A térgeometria példákat csak akkor tudod biztosan megoldani, ha:
tudod, mi a térfogat és mi a felszín, ezt látod is magad előtt.ismered a síkgeometria alakzatait (kör, négyzet, sokszög),tudod, mit jelent az átmérő, a sugár,nem okoz gondot a kerület, terület,és helyesen használod a mértékegységeket.
Én ezt az egészet egy fához hasonlítom: Tudásfa.
A törzse: síkgeometria
A koronája: térgeometria
És a gyümölcse: a pontok az érettségin.
De ha bármelyik hiányzik, ha rohad, ha nem tart – az egész dől.
Nem az a jó tanár, aki kerüli a szakszavakat. Hanem az, aki érthetően tanítja meg őket. Aki elmondja, mit jelent a szó,
aztán visszamondatja veled. Ez a fogalomépítés.
Nem szótárazás. Nem magolás.Érthető tudás.
A facebook csoportomban szerepel ez a poszt, csatlakozz és válaszolj ezekre a kérdésekre:
Te kihagytad volna ezt a feladatot?Neked mi okoz nehézséget: a képlet? A térlátás? A mértékegység? Vagy maga a szöveg?
Amikor kérdezel vagy válaszolsz, belenyúlsz a témába.
És minél jobban belenyúlsz, annál jobban érteni fogod.
Ha szeretnél egy ajándék tanítást arról, mikor kell osztani vagy szorozni a mértékegységeknél– egy olyan videót, ami segít végre ezt is átlátni, és ezzel kipipálni a Tudásfa első lépcsőfokát –akkor is csatlakozz a csoporthoz, ott tudod kérni.
Hajrá csajok!